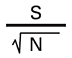If one is talking about gaming here in Connecticut, one probably means the two huge Native American-owned casinos. Gaming also is a term that has appeared in the literature to mean the ways in which a health care provider modifies an insurance claim to help ensure reimbursement or to get higher reimbursement.
The first way MCOs game their participating chiropractors is by holding them to either an arbitrary maximum number of treatments or a maximum number of treatments that comes from internal proprietary data. We have all heard from some colleague who has been reprimanded, put in a more restrictive provider tier or even removed from a panel because his or her average number of visits is higher than the MCOs average. I heard this from a colleague who only had five patients, with an average of nine visits per patient.
I started thinking about this from a statistical standpoint. For example, if an MCO says it finds that its doctors have an average of six visits per patient, then would having an average of nine visits be out of line? If the way one compares the doctor's average to the MCO's average is to say, "nine is larger than six," the answer is clearly that the doctor's average is larger than the MCO's. However, this is not proper statistically because the doctor's average is for a sample, and that is being compared to the MCO's population. Sample data cannot be directly compared with population data.
One way to do the comparison is to calculate the standard error of the mean (SEM) to help determine how far the sample's average (mean) is from the population's. Think about this: If the population's average was six and a doctor saw two patients, one for two visits and one for eight visits, the doctor's average would be six. But what if one looked at the doctor's average after he or she had seen only the eight-visit patient? The average would be eight and that would be above the norm. The SEM is one way to calculate a higher and lower limit for the sample data that estimates what the average would likely be if this doctor saw many more patients. The SEM is calculated by taking the population's standard deviation divided by the square root of the number in the sample.
If the population's standard deviation were 10 and the doctor had five patients, the SEM would be 4.5. Thus, the doctor's average should be considered to be 9 ± 4.5 and well within the MCO's reported average of six. The doctor shouldn't be considered to be out of the norm. Of course, this is predicated on a population standard deviation of 10 and only five patients. This means one needs to know the standard deviation the number of chiropractic office visits of the MCO's population of chiropractic patients. That's "proprietary information," so we'll never know.
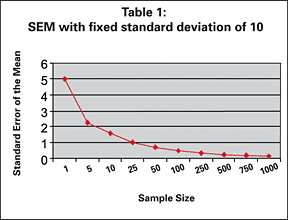
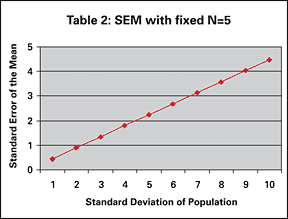
Tables 1 and 2 illustrate the change in the SEM with a different number of patients and different standard deviation of the population, respectively. As the sample size goes up, the SEM gets smaller. This makes sense because as the sample size gets larger, it is getting closer to the population size. As the standard deviation of the population gets larger, there is greater variability in the population and thus a greater possibility a sample will be further from the mean.
Thus, when the MCO says one's average is out of line with its population average, there is no way to check this without knowing the population's standard deviation. This reminds me of the way advertisers leave out information in an effort to make their products look better. Nine out of 10 dentists prefer product X. They don't tell you they only asked 10 dentists who were visiting their booth at a convention or something like that.
The second way MCOs game the doctor is just by letting the participating doctors know what the average number of chiropractic office visits are in their database. In an effort to grease the wheels, doctors make sure their practice does not bill for more visits than the MCO's average. This then artificially lowers the MCO's average and standard deviation, which then allows the MCO to reduce the acceptable number of office visits even more. Eventually, the number of office visits could get so low that if you see the patient at all, you are over the average. OK, that was a joke, but the situation is neither a joke nor is it ethical.
Finally, MCOs game doctors by requiring so much paperwork in order to get approval for additional visits that doctors just give up. It is not worth the effort to get a few more visits given the low reimbursement. It becomes more cost-effective to treat just the patient a couple of more visits for only the co-pay and never bill the MCO. Of course, this leads to the possibility that in the future, doctors will only take the co-pay and not bill at all.
By controlling the information and making the appeals process so onerous, some MCOs have done a better job than Connecticut's casinos in gaming the players. At least at the casino everyone knows what their odds are up front, and they do not change.
Click here for previous articles by Stephen M. Perle, DC, MS.